Paninimania!!
Thanks to Rodralez from LABSIN for doing all the work! 😂 Check the complete report here.
The world is clearly insane, we can all agree about that !. And the probe could be the recent madness about the infamous PANINI’s Football World cup cards. Every 4 years the madness begins!.. and this 2022 (despite all the Qatar controversy) is not going to be the exception. No Sir!
This year the PANINI album contains 638 stickers with pictures of the most worthy and wealthy 🤑 football players in the world. And of course, we have to spend our money on that. Why not? (nobody can tell me how I should spend my money!)

So, a question nobody asks is how much money I have to spend for completing the album. Nobody cares actually since Passion is beyond everything… but we care. Why do we care? Well, the fact is the question requires some math to being answering. Well, some probability theory actually.
The Coupon Collector Problem (CCP) is a mathematical framework to estimate how many coupons have to be collected to win a prize from, for example, an on-pack cereal promotion. At first glance, CCP could be used to estimate the number of missing packs to complete a PANINI album, but it is not exactly the same problem. When trying to complete a PANINI album, collectors must gather 638 stickers by getting 5 different stickers randomly when purchasing 1 pack. PANINI guarantees that stickers inside a pack are not duplicated. Additionally, PANINI collectors can cooperate and swap duplicated stickers. This is a widespread practice. Because of these particularities, this problem is usually called the PANINI Collector Problem (PCP).
A month ago, Rodralez (a recent LABSIN Member) fell into the PANINI madness and developed an online application for calculating how much money you will need to spend in this whole PANINI madness.
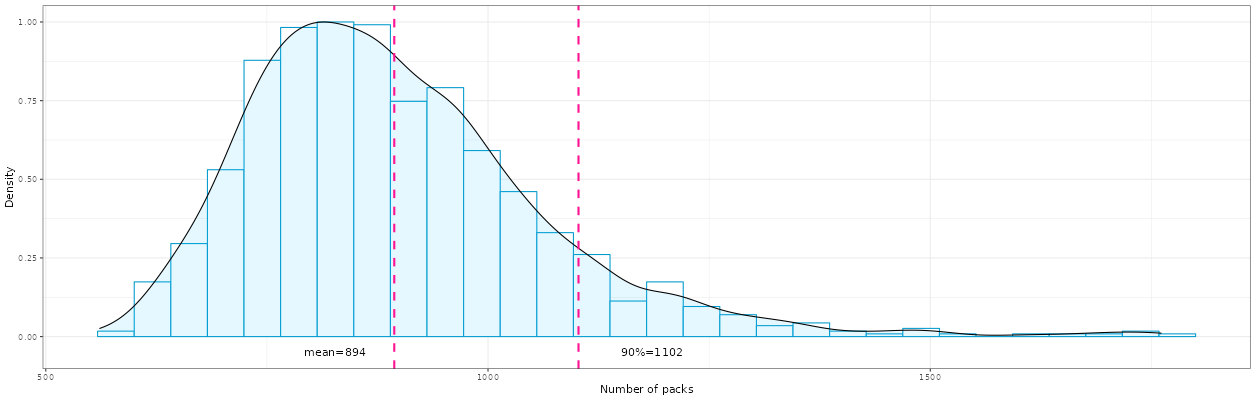
Figure 1: An estimate of probability density function (PDF) with no swapping between other collectors. On average, you need to purchase 902 packs to complete your Panini album.
The application estimates the complete probability density function (PDF) of the number of packs needed to complete a PANINI album under different scenarios. The most simple scenario assume you will buy several packets without swapping with other collectors. A very unlikely scenario (at least here in South America). For the latter, you have a closed-form solution. But the truth is that swapping with other collectors is the most common strategy for completing the album. So, the app uses Monte Carlo simulations for modeling the different swapping strategies.
Monte Carlo’s methods are perhaps the best contribution of the Grimaldi family? Well, to be honest Grimaldi had nothing to do with that of course. According to Wikipedia Monte Carlo methods were one of the first algorithms programmed into the ENIAC computer by Von Neumann and Nicholas Metropolis . The name is just an internal joke of Metropolis due to the intrinsic randomness of the algorithm.
Anyway, the app uses Monte Carlo experiments for obtaining a PDF considering swapping interaction with a different number of collectors. If you have fallen into the PANINI madness, please give it a try. It will give you information about the number of packages you need to buy and how many other collectors you need to interact with. Who knows perhaps it can help you to put yourself together and start spending your money on more useful things…? Probably not!
References
[1] Rodralez’s report describes the mathematical framework used by the APP.
[2] Link to the web app using Shiny.
[3] A master thesis focusing on PCP.
