Machine Learning Experimental Design 102
This post is part of a series of posts about experimental design in machine learning: Experimental design 101
The problem behind the split.
Shuffling your dataset and split in train/test is not always the best approach. Train and test datasets need some degree of similarity (both need to follow the same distribution), otherwise it would impossible for the model to achieve a decent performance on test (see the model performance mismatch problem). But, on the other hand, if the examples are too similar in both datasets, then you could not assure a real generalization of your model. See this post with a simple and straighforward example of wrong random splits.
Obviously, a good practice is to visualize the distribution of both (train and test) datasets. In particular the target variable distribution. However, there are some other alternatives to analyze the difference between both datasets. I run into several practical strategies, which I enumerate as follows:
The caret package for R language implements two types of split: the first uses the distribution of your target variable (dependent variable). For classification problem, you can have a certain guarantee that all your classes will be present in your testset. However, all the examples present in testset could be very similar to train and their correct class prediction could be straightforward. Alternatively, the second is based on the information provided by the descriptor variables. For creating sub–samples using a maximum dissimilarity caret implements the approach published in Willett,1999. On the other hand, this last split strategy has the problem of not guaranteeing all the classes are present in your test set. As you can see, both approaches have their pro and cons and you probably will need to implement something in between.
An interesting and straightforward technique for analyzing the differences between your train and test set is to run a model for predicting whether a given example belongs to train or test sets. If the model shows high accuracy in classifying each example to the its dataset, then we can be sure they are quite different.
Another interesting approach used for classification is to do a regression analysis using the labels from training to predict the labels from test (and vice versa). Then you can use the coefficient of determination \(R^2\) to analyze the correlation between both datasets.
If you are performing some sort of cross validation, it is interesting to remember the approach suggested in the ESL quoted below:
An obvious, but often ignored, dictum is that \(Err_{cval}\) is more believable if the test set is further separated from the training set. “Further” has a clear meaning in studies with a time or location factor, but not necessarily in general. For J -fold cross-validation, separation is improved by removing contiguous blocks of \(N/J\) cases for each group, rather than by random selection, but the amount of separation is still limited, making \(Err_{ccv}\) less believable than a suitably constructed \(Err_{cval}\).
Be caution when using Cross Validation(CV)
As stated in ESL, CV provides you with an reasonable good estimator of your model performance for unseen examples. However, such estimation can suffer when you apply a transformation to your TRAINING data. The figure below shows the classical experimental design followed when you apply some kind of transformation to your TRAINING dataset. An example of such transformation could be scaling/centering your data using the maximum value for some variable present in training dataset or (UP/DOWN)sampling for dealing with unbalanced classes. In any case, it is important that the portion of your training set used for validating during the CV remains in it original state (i.e. without any transformation). Otherwise, the CV report would not provide you with accurate information and in some cases you could finish with not necessarily the best model. (Note that stablishing the best model is a whole different problem 😱 )
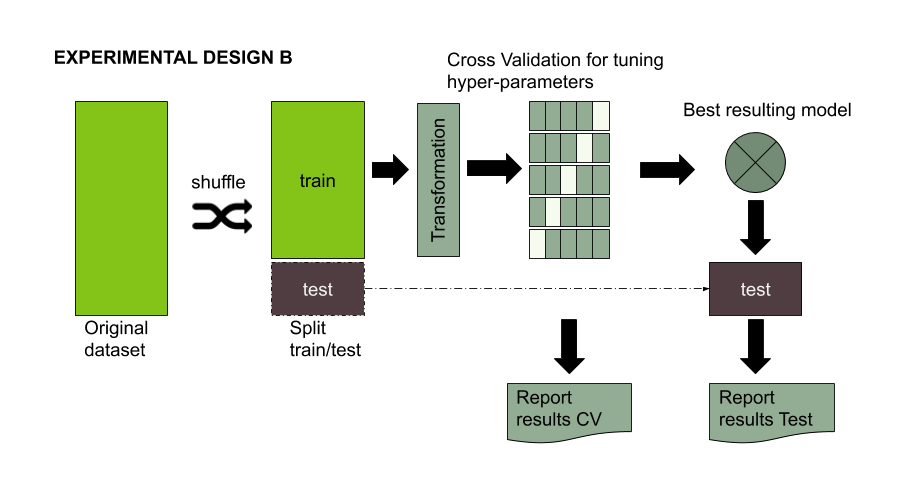
Figure 1. Standard experimental design for evaluating the performance of a machine learning model using some kind of data transformation.
Again the caret package for R language provides you with a set of tools for dealing with such situation. In particular, caret discuses the problem of down/up sampling inside resampling and according to the documentation, an estimator closer to the real model performance in test is obtained when avoiding any transformation in the k-fold used for validation.
To sum up, the same precautions you have to avoid being influenced by test set information should be followed for the k-fold used for validation during the CV. Otherwise, the whole model selection process could be affected..
